滤波器设计教程
作者: Moto Hira
本教程展示了如何创建基本的数字滤波器(脉冲响应)及其特性。
我们将探讨基于加窗 sinc 核的低通、高通和带通滤波器,以及频率采样方法。
本教程需要原型 DSP 功能,这些功能在 nightly 版本中可用。
请参考 https://pytorch.org/get-started/locally 获取安装 nightly 版本的说明。
import torch
import torchaudio
print(torch.__version__)
print(torchaudio.__version__)
import matplotlib.pyplot as plt
2.6.0
2.6.0
from torchaudio.prototype.functional import frequency_impulse_response, sinc_impulse_response
加窗Sinc滤波器
Sinc filter 是一种理想化的滤波器,它能够去除高于截止频率的频率,而不影响较低的频率。
在解析解中,Sinc filter 具有无限的滤波器宽度。在数值计算中,Sinc filter 无法精确表示,因此需要近似处理。
窗函数截断的有限脉冲响应是 Sinc filter 的一种近似。它首先针对给定的截止频率计算 sinc 函数,然后截断滤波器的边缘,并应用一个窗函数(如汉明窗)以减少截断引入的伪影。
sinc_impulse_response() 为给定的截止频率生成窗函数截断的脉冲响应。
低通滤波器
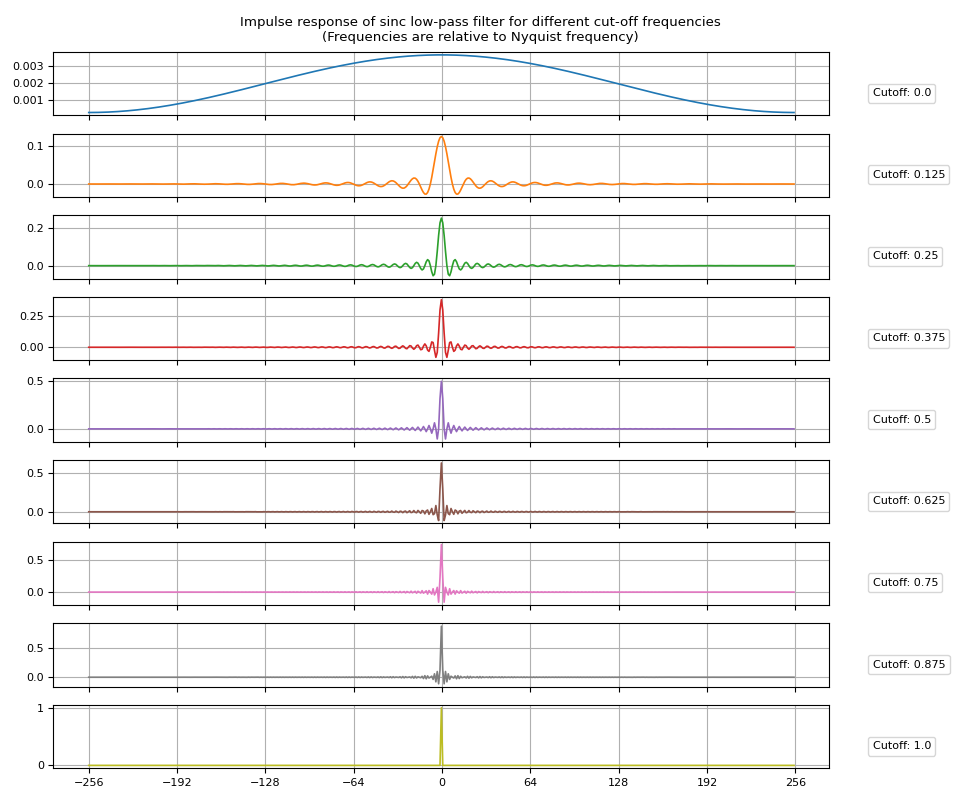
脉冲响应
创建 sinc 脉冲响应就像将截止频率值传递给 sinc_impulse_response() 一样简单。
cutoff = torch.linspace(0.0, 1.0, 9)
irs = sinc_impulse_response(cutoff, window_size=513)
print("Cutoff shape:", cutoff.shape)
print("Impulse response shape:", irs.shape)
Cutoff shape: torch.Size([9])
Impulse response shape: torch.Size([9, 513])
让我们可视化生成的脉冲响应。
def plot_sinc_ir(irs, cutoff):
num_filts, window_size = irs.shape
half = window_size // 2
fig, axes = plt.subplots(num_filts, 1, sharex=True, figsize=(9.6, 8))
t = torch.linspace(-half, half - 1, window_size)
for ax, ir, coff, color in zip(axes, irs, cutoff, plt.cm.tab10.colors):
ax.plot(t, ir, linewidth=1.2, color=color, zorder=4, label=f"Cutoff: {coff}")
ax.legend(loc=(1.05, 0.2), handletextpad=0, handlelength=0)
ax.grid(True)
fig.suptitle(
"Impulse response of sinc low-pass filter for different cut-off frequencies\n"
"(Frequencies are relative to Nyquist frequency)"
)
axes[-1].set_xticks([i * half // 4 for i in range(-4, 5)])
fig.tight_layout()
plot_sinc_ir(irs, cutoff)
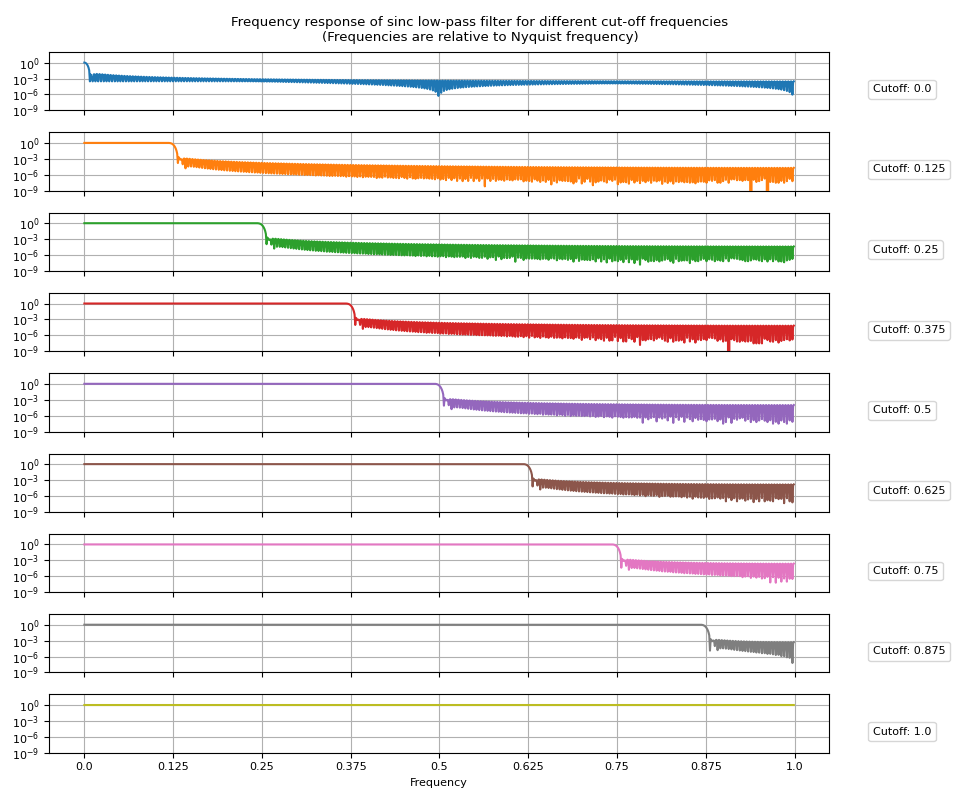
频率响应
接下来,我们来看一下频率响应。简单地对脉冲响应应用傅里叶变换即可得到频率响应。
frs = torch.fft.rfft(irs, n=2048, dim=1).abs()
让我们可视化生成的频率响应。
def plot_sinc_fr(frs, cutoff, band=False):
num_filts, num_fft = frs.shape
num_ticks = num_filts + 1 if band else num_filts
fig, axes = plt.subplots(num_filts, 1, sharex=True, sharey=True, figsize=(9.6, 8))
for ax, fr, coff, color in zip(axes, frs, cutoff, plt.cm.tab10.colors):
ax.grid(True)
ax.semilogy(fr, color=color, zorder=4, label=f"Cutoff: {coff}")
ax.legend(loc=(1.05, 0.2), handletextpad=0, handlelength=0).set_zorder(3)
axes[-1].set(
ylim=[None, 100],
yticks=[1e-9, 1e-6, 1e-3, 1],
xticks=torch.linspace(0, num_fft, num_ticks),
xticklabels=[f"{i/(num_ticks-1)}" for i in range(num_ticks)],
xlabel="Frequency",
)
fig.suptitle(
"Frequency response of sinc low-pass filter for different cut-off frequencies\n"
"(Frequencies are relative to Nyquist frequency)"
)
fig.tight_layout()
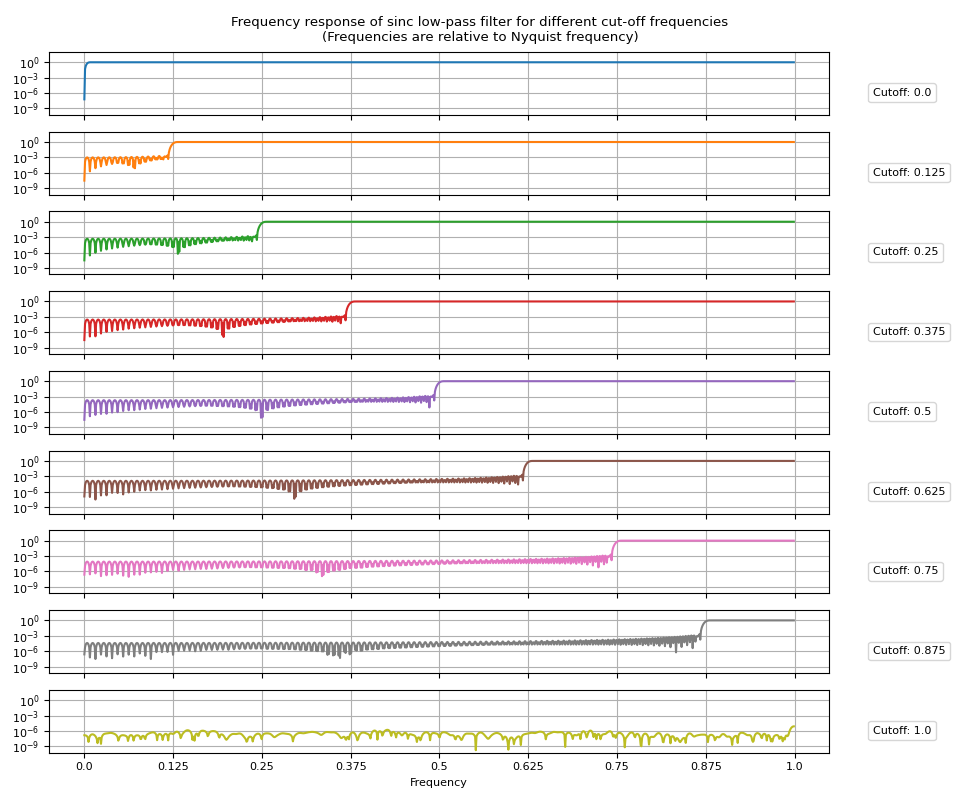
plot_sinc_fr(frs, cutoff)
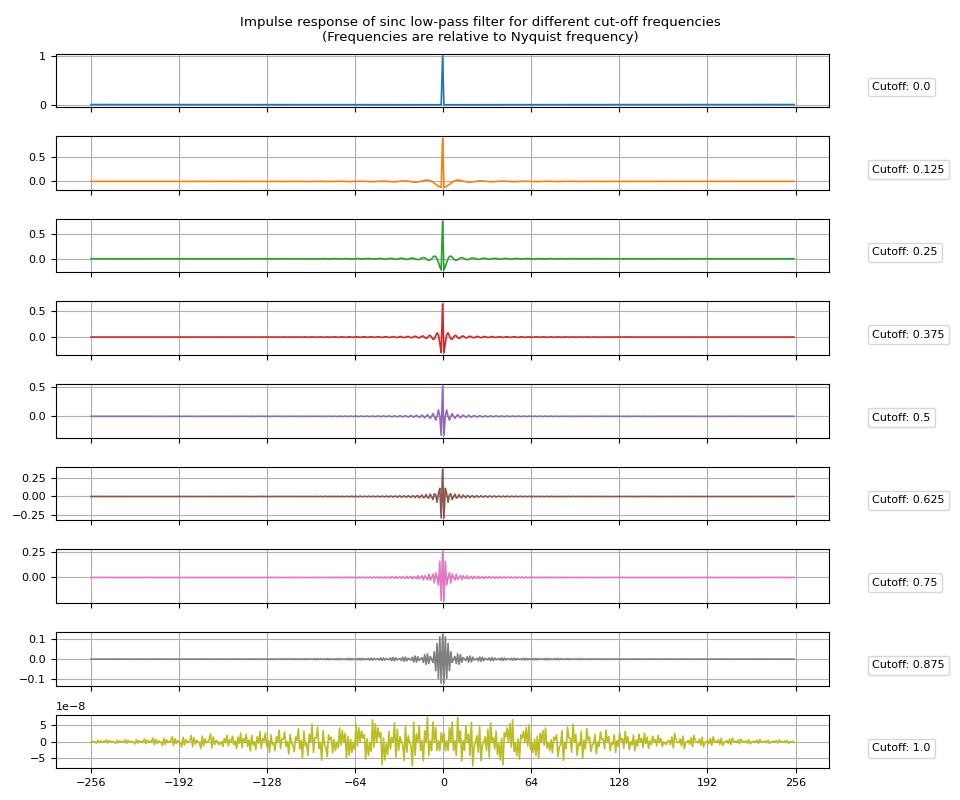
高通滤波器
高通滤波器可以通过从 Dirac delta 函数中减去低通滤波器的脉冲响应来获得。
将 high_pass=True 传递给 sinc_impulse_response() 会将返回的滤波器内核更改为高通滤波器。
irs = sinc_impulse_response(cutoff, window_size=513, high_pass=True)
frs = torch.fft.rfft(irs, n=2048, dim=1).abs()
脉冲响应
plot_sinc_ir(irs, cutoff)
频率响应
plot_sinc_fr(frs, cutoff)
带通滤波器
带通滤波器可以通过从下频带的低通滤波器中减去上频带的低通滤波器来获得。
cutoff = torch.linspace(0.0, 1, 11)
c_low = cutoff[:-1]
c_high = cutoff[1:]
irs = sinc_impulse_response(c_low, window_size=513) - sinc_impulse_response(c_high, window_size=513)
frs = torch.fft.rfft(irs, n=2048, dim=1).abs()
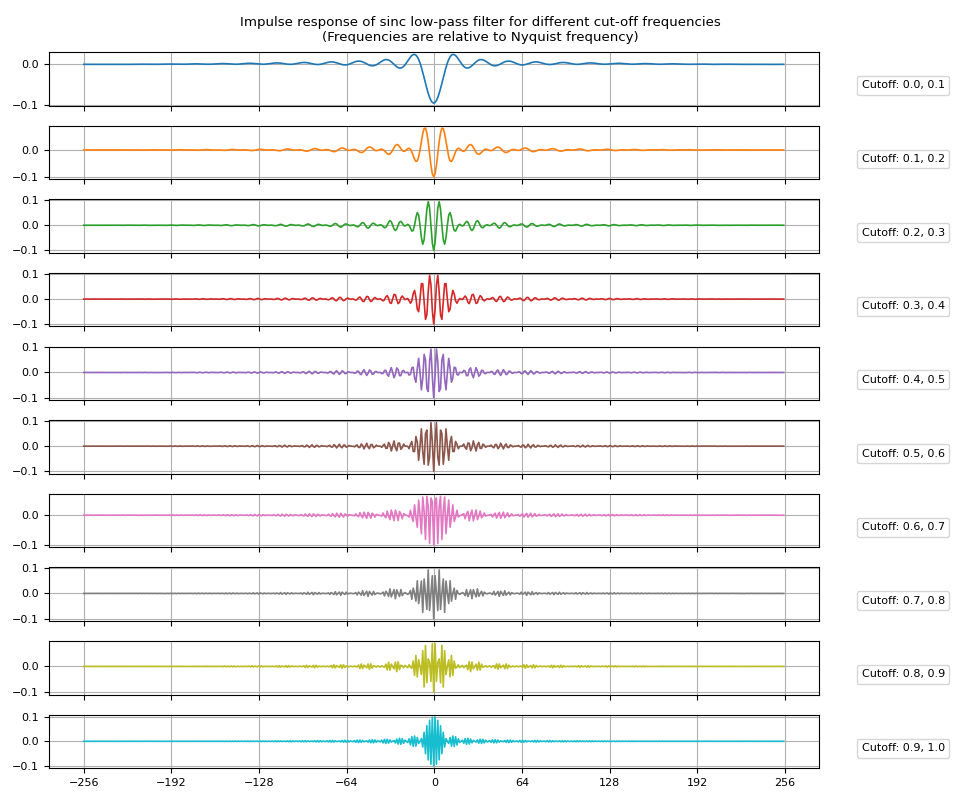
脉冲响应
coff = [f"{l.item():.1f}, {h.item():.1f}" for l, h in zip(c_low, c_high)]
plot_sinc_ir(irs, coff)
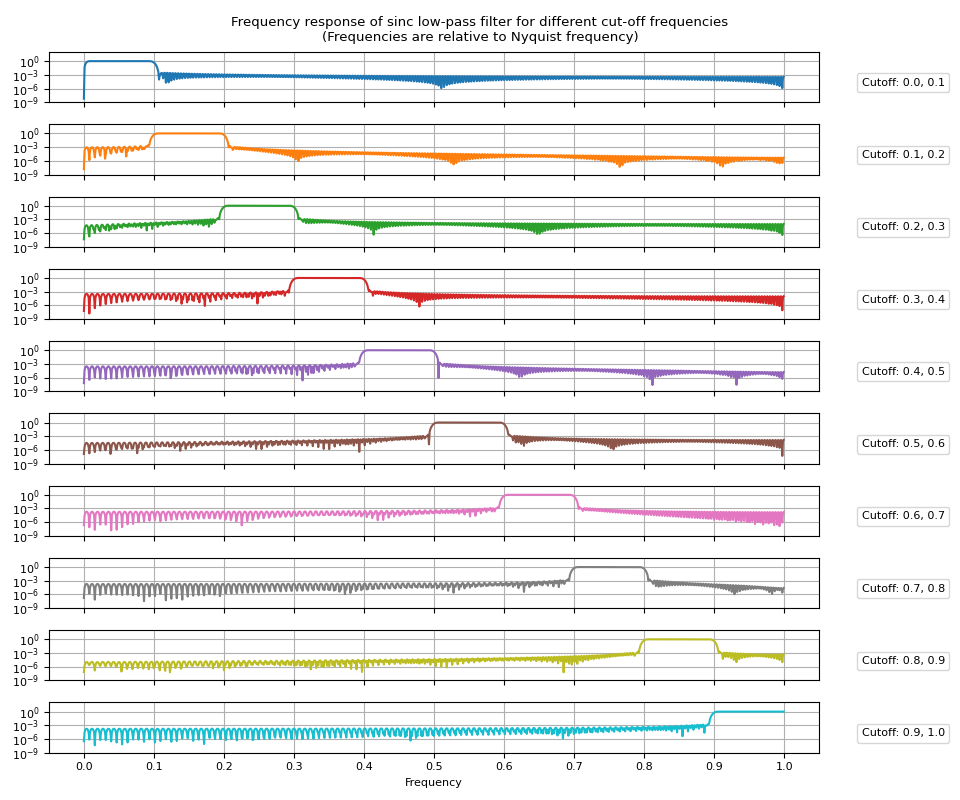
频率响应
plot_sinc_fr(frs, coff, band=True)
频率采样
我们接下来要探讨的方法是从期望的频率响应开始,通过应用逆傅里叶变换来获取脉冲响应。
frequency_impulse_response() 接收(未归一化的)频率幅度分布,并从中构建脉冲响应。
但需要注意的是,生成的脉冲响应并不会产生期望的频率响应。
在下面的内容中,我们将创建多个滤波器,并比较输入频率响应与实际频率响应。
砖墙滤波器
让我们从砖墙滤波器开始
magnitudes = torch.concat([torch.ones((128,)), torch.zeros((128,))])
ir = frequency_impulse_response(magnitudes)
print("Magnitudes:", magnitudes.shape)
print("Impulse Response:", ir.shape)
Magnitudes: torch.Size([256])
Impulse Response: torch.Size([510])
def plot_ir(magnitudes, ir, num_fft=2048):
fr = torch.fft.rfft(ir, n=num_fft, dim=0).abs()
ir_size = ir.size(-1)
half = ir_size // 2
fig, axes = plt.subplots(3, 1)
t = torch.linspace(-half, half - 1, ir_size)
axes[0].plot(t, ir)
axes[0].grid(True)
axes[0].set(title="Impulse Response")
axes[0].set_xticks([i * half // 4 for i in range(-4, 5)])
t = torch.linspace(0, 1, fr.numel())
axes[1].plot(t, fr, label="Actual")
axes[2].semilogy(t, fr, label="Actual")
t = torch.linspace(0, 1, magnitudes.numel())
for i in range(1, 3):
axes[i].plot(t, magnitudes, label="Desired (input)", linewidth=1.1, linestyle="--")
axes[i].grid(True)
axes[1].set(title="Frequency Response")
axes[2].set(title="Frequency Response (log-scale)", xlabel="Frequency")
axes[2].legend(loc="center right")
fig.tight_layout()
plot_ir(magnitudes, ir)
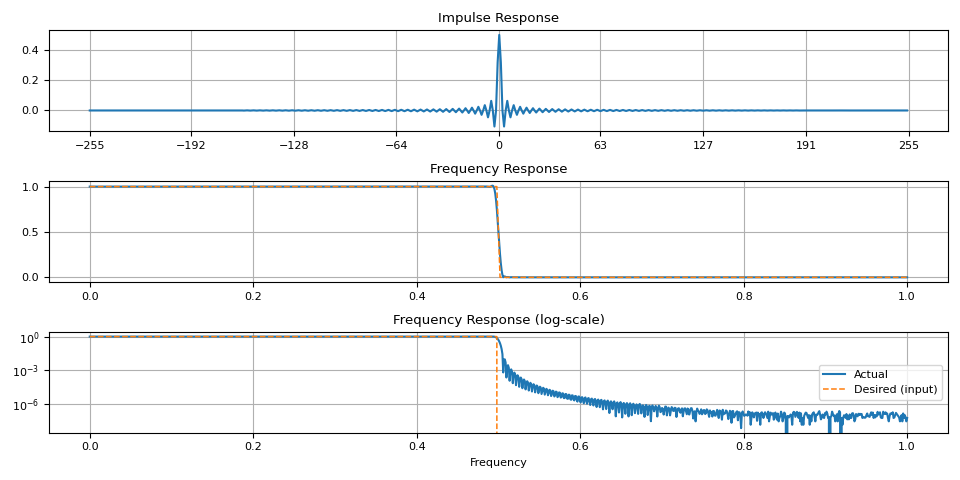
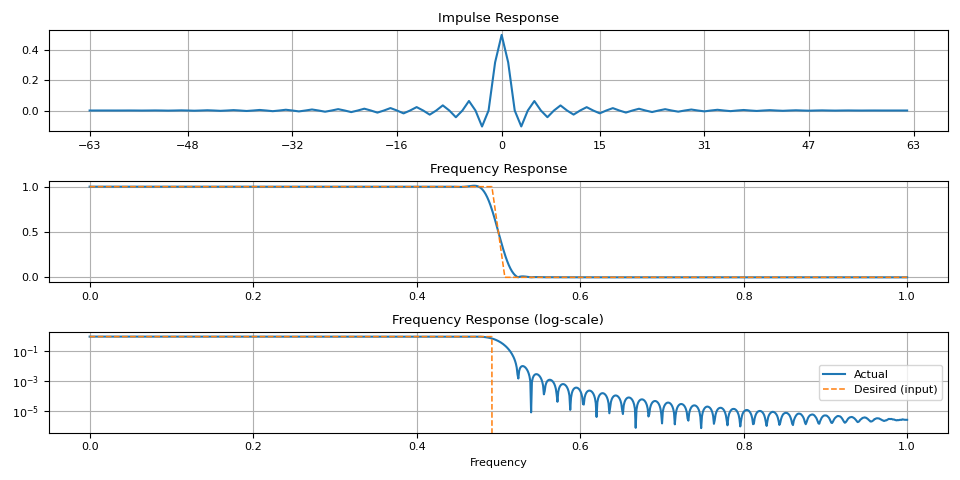
请注意,在过渡带周围存在一些伪影。当窗口尺寸较小时,这种现象更为明显。
magnitudes = torch.concat([torch.ones((32,)), torch.zeros((32,))])
ir = frequency_impulse_response(magnitudes)
plot_ir(magnitudes, ir)
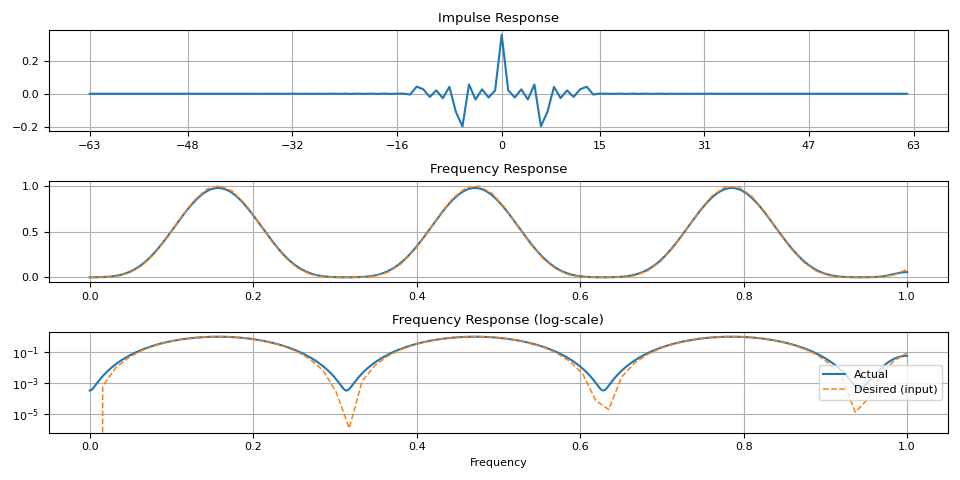
任意形状
magnitudes = torch.linspace(0, 1, 64) ** 4.0
ir = frequency_impulse_response(magnitudes)
plot_ir(magnitudes, ir)

magnitudes = torch.sin(torch.linspace(0, 10, 64)) ** 4.0
ir = frequency_impulse_response(magnitudes)
plot_ir(magnitudes, ir)